PHYSICS RESEARCH
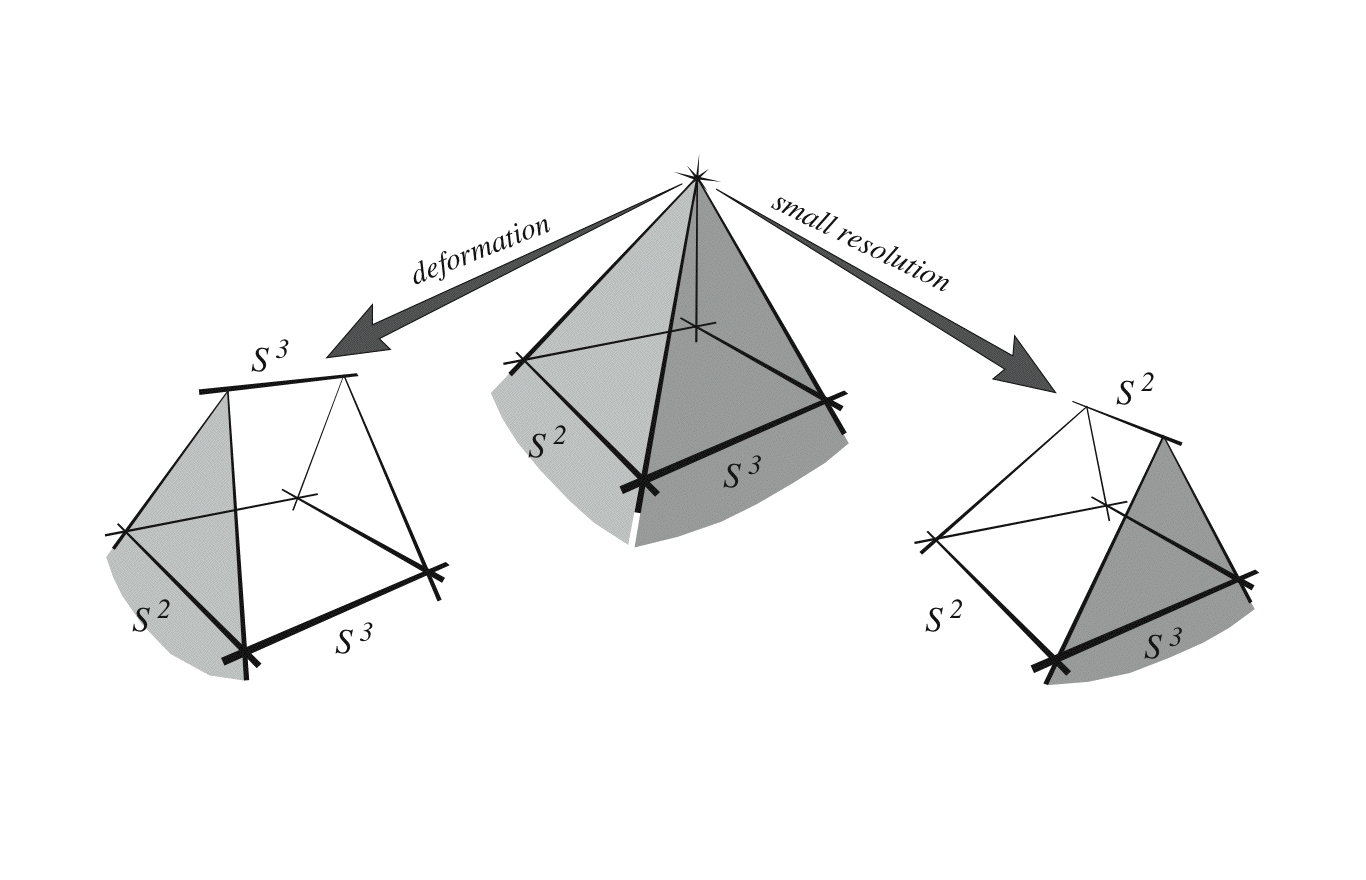
Professor Greene’s scientific research focuses on string theory, mathematical physics, and cosmology. Among his most influential contributions are the first semi-realistic models based on explicit string compactifications, the discovery of mirror symmetry, mild topology change (flop transitions), drastic topology change (conifold transitions), and early calculations of microwave background imprints of quantum gravity. Greene is the director of Columbia’s Center for Theoretical Physics.
STRING THEORY
Professor Greene’s primary field of research is string theory, a candidate for the long-sought-after theory of quantum gravity. Greene has made several influential discoveries in this field.
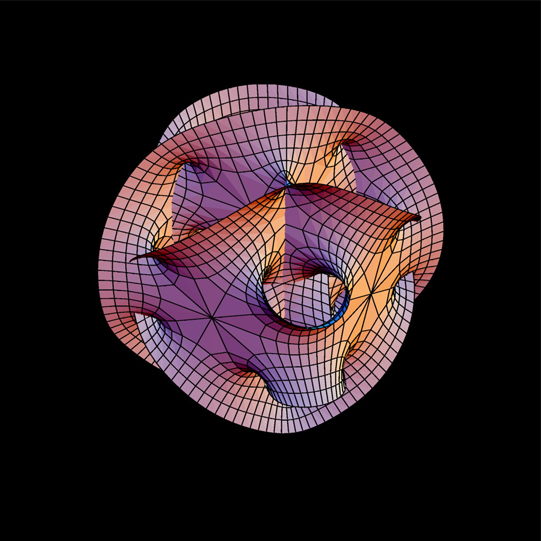
The primary goal of string theory is to unify the two pillars of modern physics, quantum mechanics and general relativity. String theory’s unification envisions that each particle in the standard model of particle physics is a different vibration of a single type of one-dimensional string. Even the graviton, the putative particle transmitting the gravitational force, would be a string, making string theory a candidate theory of quantum gravity. One of the peculiarities of string theory is that the math only works if there are more than the familiar three spatial dimensions. An explanation for why we do not perceive these additional dimensions is that they might be tightly “curled up,” into fantastically small shape, making them beyond the reach of even today’s most sophisticated technology.
GREENE’S DISCOVERIES
Professor Greene has made several influential contributions to the fields of string theory and mathematical physics.
Topology Change (Mild and Drastic)
Brian Greene is credited with the co-discovery of topology change which shows that, in string theory—unlike the case for classical general relativity—it is possible for spacetime to tear and in that way undergo a fundamental change in shape.
Mirror Symmetry
One of Brian Greene’s most famous discoveries is mirror symmetry, which shows that two distinct geometrical forms for spacetime in string theory can yield identical physical implications—a result that has had deep impact in both physics and mathematics.
Greene’s Other Discoveries
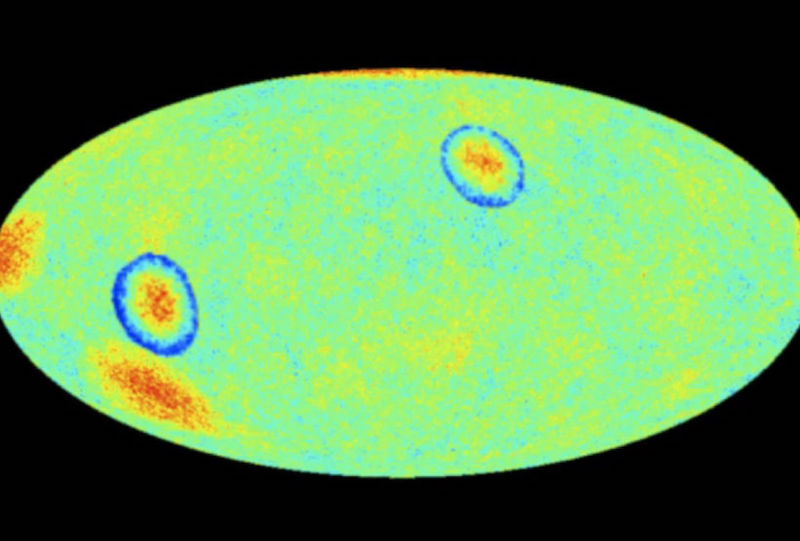
Greene’s contributions also include developing methods to link string theory with observable physics, including some of the earliest semi-realistic models based on explicit string compactifications and the first calculations of potential cosmic microwave background imprints of quantum gravity.
Because string theory requires extra spatial dimensions, the mathematics describing how these dimensions “curl up” is an important area of research. Brian Greene and collaborators constructed the first low-energy string models derived from explicit Calabi-Yau compactifications, and also calculated possible imprints of a shortest distance scale on CMB temperature anisotropies.
